Simple 3-Way Active Crossover Circuit Diagram

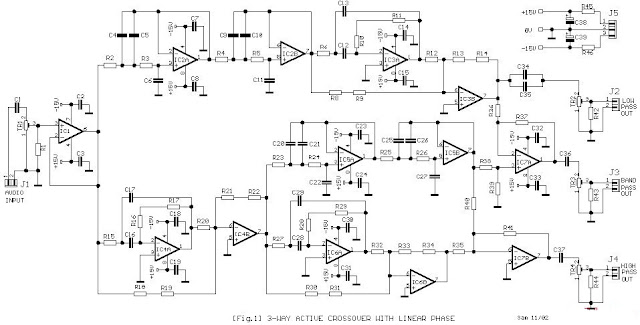
This is the Simple 3-Way Active Crossover Circuit Diagram with linear phase response. The problems that exist at common crossover circuit is known. The low pass filter causes a delay in the signal. Unlike the high-pass filter causes a head in the signal passing through it. Thus the frequency separation created some problems such as:

1. Signals of the two filters are mutually exclusive
2. The phase shift between the filter affects the radiation
3. The radiation pattern depends on the frequency

The crossover circuit tries to solve many of the problems mentioned above and based on a study of S. Lipshitz and J.  Vanderkooy, published in the JAES (Journal Audio Engineering Society). A lattice separation uses a linear phase low-pass section with the help of a time delay circuit and a circuit removal gives the output signal with high-pass filter characteristics. The time delay is not constant over the entire frequency range, but changing very slowly and mainly there are phase differences between signals of the two charges, not even close to the crossover.

Simple 3-Way Active Crossover Circuit Diagram

The circuit consists separation as shown in block diagram [Fig.2] two low pass filters of fourth grade, -24db/oct for a line of low-frequency signals and one for the high frequency separation. In the same frequencies operate both units delay time T1 (for low frequency F1) and T2 (for high frequency F2) and give the same phase characteristics of the low pass section.

The delay circuit T1 simulates the time delay introduced by low-frequency filter LPF1, while T2 simulates the time delay introduced by low-frequency filter LPF2 that exists in the line of midrange. Then the signal from the low pass filter removed [IC7A-B] of the signal has been delayed, a clear signal that the characteristics are the same as a signal that has passed through a high pass filter. At the exit of each line is a trimmer with which we can adjust the level between the levels of loudspeakers. The power circuit is a well-stabilized voltage + /-15V. The use of meshed split fourth order Linkwitz forcing crossovers be located at-6db [Fig.3].

The above picture shows the main circuits and the necessary formulas for calculating the low pass filters as well as trusses time delay. There is also an example calculation for crossovers and 200IZ 3KIZ that will help calculate and adjust to your needs. The circuit derived from a relevant article of the magazine Elektor. 

Components List:
R1,16 = 100Kohms
R2,3,4,5 = 56Kohms
R6,27 = 37.5Kohms[33K+4.7K]
R8,9,12,13,14 = 10Kohms
R10,28 = 75Kohms (150K//150K)
R11,29 = NC
R15 = 56.3Kohms
R17 = 12Kohms
R18,19,20,21,22 = 10Kohms
R23,24,25,26 = 37.5Kohms [33K+4.7K]
R30,31,32,33,34,35,36 = 10Kohms
R37,38,39,40,41,41 = 10Kohms
R42,43,44 = 47Kohms
R45,46 = 47 ohms
TR1,2,3,4 = 47Kohms trimmer or pot.
C1,34,35 = 2.2uF 100V MKT
C2,3,7,8,14,15,18 = 47nF 100V MKT
C4,5,6,9,10,11,16,17 = 10nF 100V MKT
C12,13,20,21,22 = 1nF 100V MKT
C19,23,24,30,31,32,33 = 47nF 100V MKT
C25,26,27,28,29 = 1nF 100V MKT
C36,37 = 1uF 100V MKT
C38,39 = 47uF 25V
IC1 = TL071
IC2,3,4,5,6,7 = TL072,NE5532
All the resistors is 1/4W 1% metal film

Sourced by Elektor